Association Rules Mining

Synonym: Market basket analysis

Source: www.quickmeme.com

Itemsets

  • Items \(I\): The set of available items \(I = \{i_1, ..., i_M\}\)
  • Itemset \(X\): A set of items \(X \subseteq I\)
  • Itemset size \(K\): The number of items in the itemset
  • \(K\)-itemset: An itemset of size \(K\)
  • Items are ordered: \[X_n=\{x_1, x_2, ...,x_K\}, \text{ such that } x_1 \leq x_2 \leq ... \leq x_K\]

Transactions

  • Transaction: \(T_n=(tid, X_{\text{tid}})\)
  • Transactions in database: \(\{T_1, T_2, ..., X_N\}\)
tid itemset
1 {apple, bread, honey, milk, peanuts}
2 {bread, chips, coke, honey, milk}
3 {bread, chips, coke, honey, steak}
...
8 {apple, bread, cheese, milk, peanuts}

Support

  • \(s(X)\): fraction of transactions that contain \(X\) \[s(\{bread, milk\}) =\ ?\] \[s(\{chips, coke\}) =\ ?\]

Example

tid itemset
1 {apple, bread, honey, milk, peanuts}
2 {bread, chips, coke, honey, milk}
3 {bread, chips, coke, honey, steak}
4 {apple, coke, honey, milk, peanuts}
5 {bread, chips, coke, honey, milk}
6 {apple, chips, coke, milk}
7 {apple, bread, coke, milk, peanuts}
8 {apple, bread, cheese, milk, peanuts}

Frequent Itemsets Mining (FIM)

  • An itemset \(X\) is frequent if its support in the DB is greater or equal than a minimum support threshold \(t_s\): \[s(X) \geq t_s\]

  • Given:

    • Set of items \(I\)
    • Transaction database over \(I\)
    • Minimum support threshold \(t_s\)

  • Goal: Find all frequent itemsets \(\{X \subseteq I | s(X) \geq t_s\}\)

FIM - example

tid items
2000 {A,B,C}
1000 {A,C}
4000 {A,D}
5000 {B,E,F}
  • Support of 1-itemsets:

(A): 75%, (B), (C): 50%, (D), (E), (F): 25%

  • Support of 2-itemsets:

(A, C): 50%,
(A,B), (A,D), (B,C), (B,E), (B,F), (E,F): 25%

Association rules

Let \(X\), \(Y\) be two itemsets: \(X,Y \subseteq I\) and \(X \cap Y=\emptyset\).

  • Association rules represent implications of the form \(X \rightarrow Y\)

  • Support of a rule: The fraction of transactions containing \(X \cup Y\)
    \[s(X \rightarrow Y)=s(X \cup Y)\]

  • Confidence \(c\) of a rule: the fraction of transactions containing \(X \cup Y\) in the set of transactions containing \(X\). \[c(X \rightarrow Y)=\frac{s(X \cup Y)}{s(X)}\]

Association Rule Mining (ARM)

  • Given:
    • Set of items \(I\)
    • Transaction database over \(I\)
    • Minimum support threshold \(t_s\) and a minimum confidence threshold \(t_c\)
  • Goal: Find all association rules \(X\rightarrow Y\) in DB with minimum support threshold and a minimum confidence i.e.: \[\{X\rightarrow Y | s(X \cup Y) \geq t_s, c(X\rightarrow Y)\geq t_c \}\] These rules are called strong.

ARM - example

tid items
2000 {A,B,C}
1000 {A,C}
4000 {A,D}
5000 {B,E,F}

Association rules:

  • \(A\rightarrow C\):

\(s(A\rightarrow C)=0.50, c(A\rightarrow C)=0.67\)

  • \(C\rightarrow A\):

\(s(C\rightarrow A)=0.50, c(C\rightarrow A)=1.0\)

Finding Strong Association Rules

  1. FIM: Find the frequent itemsets w.r.t. minimum support threshold.
  2. ARM: Find strong association rules among the frequent itemsets.

FRM by brute-force is inefficient

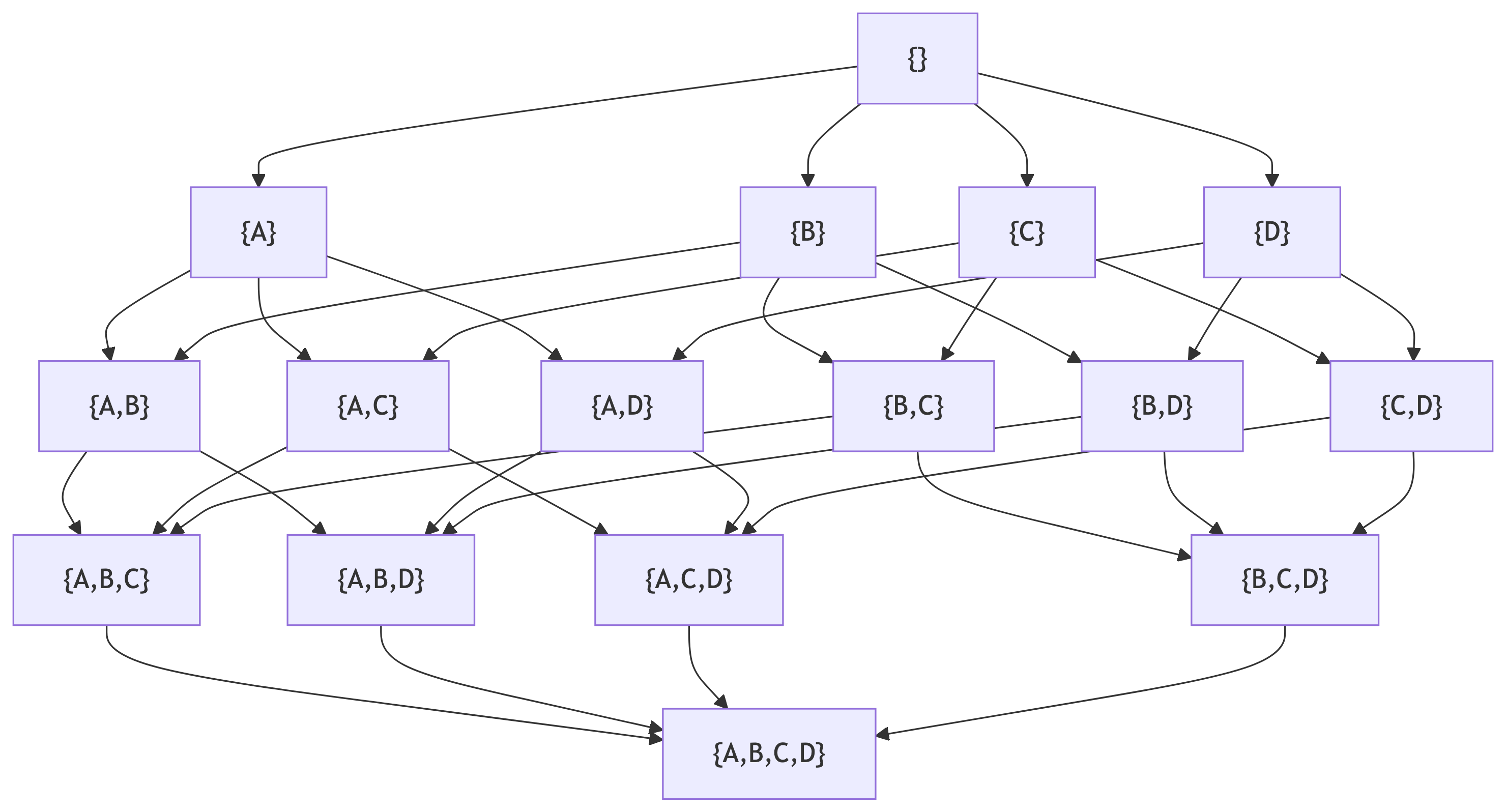
Example with small set of items: \(I = \{A,B,C,D\}\)

  • # 1-itemsets: \(\binom{4}{1} = \frac{4!}{1!(4-1)!}=\frac{4!}{3!}=4\)
  • # 2-itemsets: \(\binom{4}{2} = \frac{4!}{2!(4-2)!}=\frac{4!}{2!2!}=6\)
  • # 3-itemsets: \(\binom{4}{3} = \frac{4!}{3!(4-3)!}=\frac{4!}{3!}=4\)
  • # 4-itemsets: \(\binom{4}{4} = \frac{4!}{4!(4-4)!}=1\)

In general for \(|I|\) items: \(\binom{|I|}{1} + \binom{|I|}{2} + ... + \binom{|I|}{K} = 2^{|I|}-1\) itemsets

Apriori Algorithm

Reduces the candidate itemsets to be tested: If an itemset is frequent, then all of its subsets must also be frequent. And if an itemset is infrequent, its supersets must not be tested.

Initialise: \(k=1\). Scan DB to get frequent 1-itemsets

Repeat:

  1. Set \(k=k+1\)
  2. generate length \(k\) candidate itemsets from length \(k-1\) frequent itemsets
  3. test the candidates against DB to get frequent \(k\)-itemset
  4. Stop when no frequent or candidate set was generated in 3.

Example

  • Database with 9 transactions
  • Minimum support \(t_{s}=22\%\)
  • Minimum confidence \(t_c=70\%\)
    1. Identify frequent itemsets using Apriori
    1. Identify association rules
Database
tid items
1 {chips, coke, whiskey}
2 {beer, chips}
3 {chips, ice}
4 {beer, chips, coke}
5 {coke, ice}
6 {chips, ice}
7 {coke, ice}
8 {chips, ice, coke, whiskey}
9 {chips, coke, ice}

Example - \(k=1\)

Database
tid items
1 {chips, coke, whiskey}
2 {beer, chips}
3 {chips, ice}
4 {beer, chips, coke}
5 {coke, ice}
6 {chips, ice}
7 {coke, ice}
8 {chips, ice, coke, whiskey}
9 {chips, coke, ice}
Candidates \(C_1\)
itemset \(s\)
{coke} 67%
{chips} 78%
{ice} 67%
{beer} 22%
{whiskey} 22%
Frequent itemsets \(L_1\)
itemset \(s\)
{coke} 67%
{chips} 78%
{ice} 67%
{beer} 22%
{whiskey} 22%

Generate candidates

\(C_k\) is generated by

  1. Self-joining \(L_{k-1}\): \(L_{k-1} \cdot L_{k-1}\). Two \((k-1)\)-itemsets are joined, if they agree in the first \((k-2)\) items
  2. Pruning all \(k\)-itemsets with a \((k-1)\)-subset that is not frequent, i.e. not in \(L_{k-1}\)

Example: \(L_3=\{abc, abd, acd, ace, bcd\}\)

  1. \(C_4=L_3 \cdot L_3=\{abc \cdot abd=abcd, acd\cdot ace=acde\}\)
  2. \(acde\) is pruned since \(cde\) is not in \(L_3\)

Example - \(k=2\)

Generate \(C_2\) by self-joining \(L_1\), determine \(s\) and prune by support threshold \(\rightarrow L_2\)

Database
tid items
1 {chips, coke, whiskey}
2 {chips, beer}
3 {chips, ice}
4 {coke, chips, beer}
5 {coke, ice}
6 {chips, ice}
7 {coke, ice}
8 {coke, chips, ice, whiskey}
9 {coke, chips, ice}
Candidates \(C_2\)
itemset \(s\)
{beer, chips} 22%
{beer, coke} 11%
{beer, ice} 0%
{beer, whiskey} 0%
{chips, coke} 44%
{chips, ice} 44%
{chips, whiskey} 22%
{coke, ice} 44%
{coke, whiskey} 22%
{ice, whiskey} 11%
Frequent itemsets \(L_2\)
itemset \(s\)
{beer, chips} 22%
{chips, coke} 44%
{chips, ice} 44%
{chips, whiskey} 22%
{coke, ice} 44%
{coke, whiskey} 22%

Example - \(k=3\)

Generate \(C_3\) by self-joining \(L_2\), determine \(s\) and prune by support threshold \(\rightarrow L_3\)

Candidates \(C_3\)
itemset \(s\)
{chips, coke, ice} 22%
{chips, coke, whiskey} 22%
{coke, ice, whiskey} 11%
Frequent itemsets \(L_3\)
itemset \(s\)
{chips, coke, ice} 22%
{chips, coke, whiskey} 22%

Example - \(k=4\)

Self-joining \(\rightarrow C_3=\emptyset \rightarrow\) stop

Identify Association Rules

  • For every frequent itemset \(X\)
    • For every subset \(Y: Y\neq \emptyset, Y\neq X\), form the rule \(Y\rightarrow (X - Y)\)
    • Remove rules with \(c(Y\rightarrow (X - Y))=\frac{s(X)}{s(Y)}\lt t_c\)

Example - Association Rules

From \(L_2\):

  • \(\text{\{beer\}} \rightarrow \text{\{chips\}}: c = \frac{s(\{\text{beer, chips\}})}{s(\text{\{beer\}})} = \frac{22\%}{22\%} = 100\%\)
  • \(\text{\{beer\}} \rightarrow \text{\{chips\}}: c = \frac{s(\text{\{beer, chips\}})}{s(\text{\{chips\}})} = \frac{22\%}{78\%} = 28\%\)
  • \(\text{\{chips\}} \rightarrow \text{\{coke\}}: c = \frac{s(\text{\{chips, coke\}})}{s(\text{\{chips\}})} = \frac{44\%}{78\%} = 56\%\)
  • …

From \(L_3\):

  • \(\text{\{chips, coke\}} \rightarrow \text{\{ice\}}: c = \frac{s(\text{\{chips, coke, ice\}})}{s(\text{\{chips, coke\}})} = \frac{22\%}{44\%} = 50\%\)
  • \(\text{\{chips, ice\}} \rightarrow \text{\{ccoke\}}: c = \frac{s(\text{\{chips, coke, ice\}})}{s(\text{\{chips, ice\}})} = \frac{22\%}{44\%} = 50\%\)
    …
  • \(\text{chips\}} \rightarrow \text{\{coke, ice\}}: c = \frac{s(\text{\{chips, coke, ice\}})}{s(\text{\{chips\}})} = \frac{22\%}{78\%} = 28\%\)
    …
  • \(\text{whiskey} \rightarrow \text{\{chips, coke\}}: c = \frac{s(\text{\{chips, coke, whiskey\}})}{s(\text{\{whiskey\}})} = \frac{22\%}{22\%} = 100\%\)

The Efficient Apriori Package

from efficient_apriori import apriori
transactions = [('eggs', 'bacon', 'soup'),
                ('eggs', 'bacon', 'apple'),
                ('soup', 'bacon', 'banana')]
itemsets, rules = apriori(transactions, min_support=0.5,  min_confidence=1)
print(rules)  # [{eggs} -> {bacon}, {soup} -> {bacon}]

Beyond the Apriori Algorithm

Computational challenge: Multiple scans of transaction database required. Problematic with growing number of transactions and candidate itemsets.

Possible improvements:

  • Reduce database scans
  • Shrink number of candidate itemsets

Frequent Pattern Tree: Allows frequent itemsets discovery without candidates generation.

Summary Association Rules Mining

  • Identifes item combinations frequently appearing together across all transactions, not grouped by users
  • Does not take into account ratings
  • Does not allow to build a latent representation of users and/or items
  • → does not offer personalisation